CS194 Final Projects

Xuxin Cheng CS194-agv

Project 1 Gradient-Domain Fusion

The primary goal of this project is to seamlessly blend an object or texture from a source image into a target image. The simplest method would be to just copy and paste the pixels from one image directly into the other. Unfortunately, this will create very noticeable seams, even if the backgrounds are well-matched. How can we get rid of these seams without doing too much perceptual damage to the source region?

One way to approach this is to use the Laplacian pyramid blending technique we implemented for Proj2. Here we take a different approach. The insight we will use is that people often care much more about the gradient of an image than the overall intensity. So we can set up the problem as finding values for the target pixels that maximally preserve the gradient of the source region without changing any of the background pixels.

1.1 Toy Problem

In this part, we are going to get familiar with gradient domain processing by reconstructing an image from boundary conditions and gradient objectives. we'll compute the x and y gradients from an image s, then use all the gradients, plus one pixel intensity, to reconstruct an image v. For each pixel, then, we have two objectives:

	objective	note
1	$\min(v(x+1, y)-v(x,y) - (s(x+1,y)-s(x,y)))^2$	the x-gradients of v should closely match the x-gradients of s
2	$\min(v(x, y+1)-v(x,y) - (s(x,y+1)-s(x,y)))^2$	the y-gradients of v should closely match the y-gradients of s
3	$\min(v(1,1)-s(1,1))^2$	The top left corners of the two images should be the same color

where v(x,y) is the pixel intensity we want to get by solving least square, s(x,y) is the pixel intensity of the orginal image.

$A$ took too much memory. Then I turned to Scipy's sparse matrix and least square solver for better efficiency. The result is as follows.

SSD(Sum Square Difference) $SSD=2.93e-18$ $SSD=0.0366$ . Although using a dense matrix appears to have better performance, we would like to gain efficiency increase at an ignorable cost of precision.

1.2 Poisson Blending

Poisson blending is similar to what we have done in 1.1. The objective is as follows:

\begin{align*} \mathbf{v}=\underset{\mathbf{v}}{\operatorname{argmin}} \sum_{i \in S, j \in N_{i} \cap S}\left(\left(v_{i}-v_{j}\right)-\left(s_{i}-s_{j}\right)\right)^{2}+\sum_{i \in S, j \in N_{i} \cap \neg S}\left(\left(v_{i}-t_{j}\right)-\left(s_{i}-s_{j}\right)\right)^{2} \end{align*}

$v_i$ $i_{th}$ $s_i$ $t_i$ are intensity of the corresponding pixel in source image and target image.

$A$ $b$ $b$ $A$ s such we only need to solve least square once. The results are as follows:

We can see that the blending for the last image is not good. This is due to the face color of Trump is too different from that of an orange. Also in the third image, the leg of the goat is kind of a green color. This is also due to that the surrounding area of the leg of the source image is different from that of the target image. So when we use Poisson blending we want to make sure the background color in source and target image is as close as possible.

1.3 Bells & Whistles: Mixed Gradients

The difference of using Mixed Gradients is that we will use the gradient in source or target with the larger magnitude as the guide, rather than the source gradient as in the following objective:

\mathbf{v}=\underset{\mathbf{v}}{\operatorname{argmin}} \sum_{i \in S, j \in N_{i} \cap S}\left(\left(v_{i}-v_{j}\right)-d_{i j}\right)^{2}+\sum_{i \in S, j \in N_{i} \cap \neg S}\left(\left(v_{i}-t_{j}\right)-d_{i j}\right)^{2}

$d_{ij}$ is the value of the gradient from the source or the target image with larger magnitude, i.e. if abs(s_i-s_j) > abs(t_i-t_j), then d_ij = s_i-s_j; else d_ij = t_i-t_j. The results are as follows:

We can see that in the first blending, the texture is retained on Trump's face. In the third blending, the Cal log appears to be original of the t-shirt. Mixed blending works better where we want to retain the texture of background.

What I have Learned

By far I have learned 3 ways of blending two images: Laplacian blending, Poisson blending and Mixed Gradients blending. We can implement these methods to generate quite cool images, which makes me exciting. And I also see the advantage and disadvantage of different methods so that I can explore and develop new methods to have better performance. I also learned how to sparse matrices in Python to boost up computing and save memory.

Project 2 Augmented Reality

In this augmented reality project, we will capture a video and insert a synthetic object into the scene! The basic idea is to use 2D points in the image whose 3D coordinates are known to calibrate the camera for every video frame and then use the camera projection matrix to project the 3D coordinates of a cube onto the image. If the camera calibration is correct, the cube should appear to be consistently added to each frame of the video.

2.1 Setup

$\times$ $\times$ 40mm and drew a regular pattern on the box. I chose 20 points from the pattern, and labeled their corresponding 3D points. The input video is shown below:

2.2 Choosing Key-points and Propagating to other Images in the Video

I used cv2.TrackerMedianFlow_create() to track key-points. For each keypoint there is individual tracker. I used an 17x17 patch centered around the marked point to initialize the tracker. Then I created a new video to visualize tracking performance. The result is shown below:

2.3 Calibrating the Camera

Just like what we did in Proj5, we use least squares to compute the projection matrix:

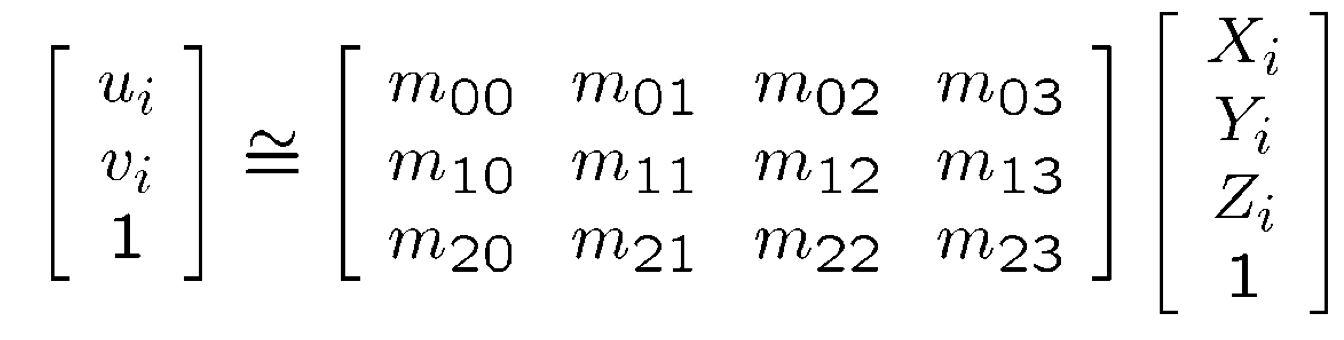
With some transformation we could write the above equation as:

\begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = \begin{bmatrix} x_i&y_i&z_i&1&0&0&0&0&0&0&0&0 \\ 0&0&0&0&x_i&y_i&z_i&1&0&0&0&0 \\ 0&0&0&0&0&0&0&0&x_i&y_i&z_i&1 \end{bmatrix} \begin{bmatrix} m_{00}\\m_{01}\\m_{02}\\m_{03}\\m_{10}\\m_{11}\\m_{12}\\m_{13}\\m_{20}\\m_{21}\\m_{22}\\m_{23} \end{bmatrix}

$m_{00}...m_{23}$ $A$ $A\in{R^{75\times 12}}$ $b\in{R^{75}}$ $\Pi$ for each frame.

2.4 Projecting a cube in the Scene

$\Pi$ and homogenous 3-D coordinate to get homogenous 2-D coordinate. Then following the description here, we are able to draw a cube at a location we want in the 3-D world. The video is shown below:

What I have learned

This project is actually more fun compared with previous projects. By simply solving for a linear projection matrix, we are able to project 3-D world coordinates to 2-D image coordinates. Later I will explore how to further decompose the projection matrix into intrinsics, projection, rotation and translation matrices.

*much material adapted from project webpage